一、平面连杆机构设计的基本问题

在生产实践中，平面连杆机构设计的基本问题可归纳为两大类：

（1）实现给定从动件的运动规律。即当原动件运动规律已知时，设计一个机构使其从动件（连杆或连架杆）能按给定的运动规律运动。如要求从动件按照某种速度运动，或具有一定的急回特性，或占据几个预定位置等。

（2）实现给定的运动轨迹。即要求机构在运动过程中连杆上某一点能实现给定的运动轨迹。如要求起重机中吊钩的轨迹为一条直线，搅拌机中搅拌杆端能按预定轨迹运动等。

二、按给定的行程速比系数K设计

设已知行程速比系数K，摇杆长度l_CD，最大摆角ψ，试设计一曲柄摇杆机构。

设计过程如下图所示，具体设计步骤如下：

（1）先按照公式，计算极位夹角θ。

（2）选取适当的比例尺μ_l，任取一点D，并以此点为顶点作等腰三角形，使两腰之长等于μ_l l_CD，∠C₁DC₂＝ψ。

（3）连接C₁、C₂，作C₂M⊥C₁C₂，再作C₁N使∠C₁C₂N＝90°－θ，C₂M与C₁N交于点P。

（4）以PC₁为直径作一辅助圆，则在圆弧C₁PC₂上任取一点A，连接AC₁、AC₂，∠C₁AC₂＝θ，所以曲柄回转中心A应在此圆弧上。

（5）由和，确定出曲柄长度l_AB和连杆长度l_BC。

（6）由图直接量取AD的长度，再按比例计算出实际长度l_AD。

 

微课

平面四杆机构设计（已知K）

三、按给定连杆位置设计

如下图所示，设已知连杆的长度l_BC，及机构在运动过程中要求占据的两个给定位置B₁C₁、B₂C₂，试设计此铰链四杆机构。

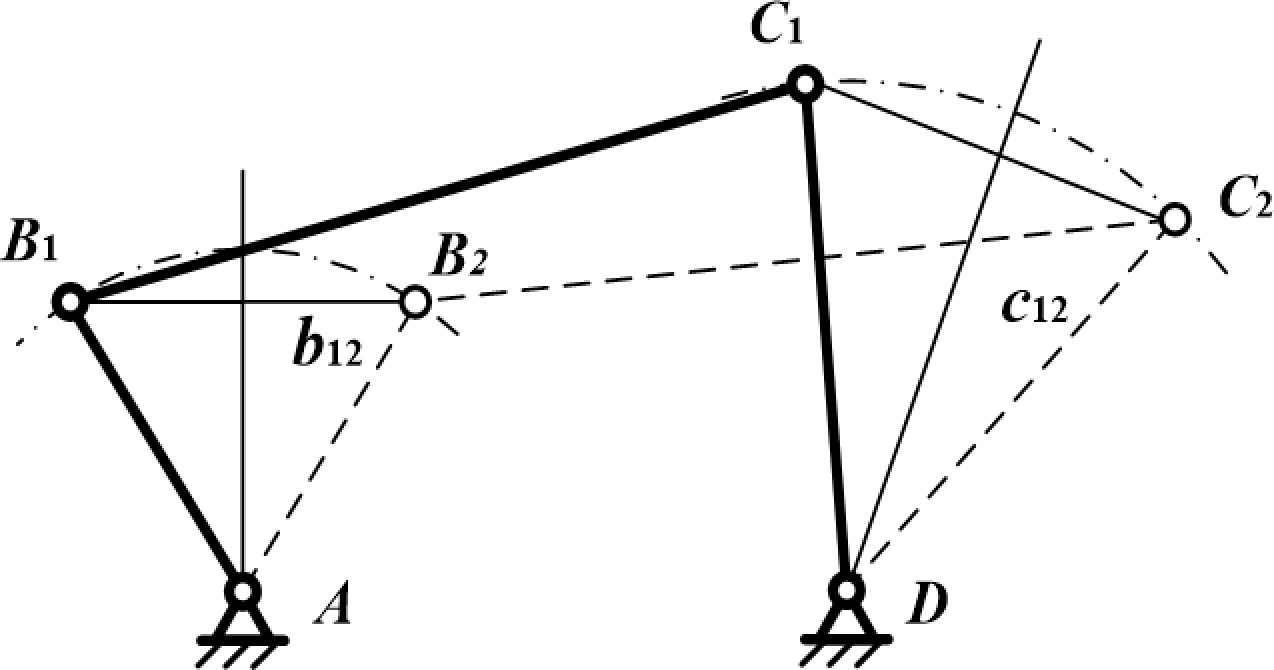
分析：设计这个机构的主要问题是，根据已知条件确定固定铰链中心A、D的位置。由于连杆上B、C两点的运动轨迹分别是以A、D为圆心，以l_AB、l_CD为半径的圆弧，所以A和D的位置必在线段B₁B₂和C₁C₂的垂直平分线b₁₂和c₁₂上，但由于l_AB和l_CD未知，故此题有无穷多解。实际在设计时，一般考虑辅助条件，如机架位置、两连架杆所允许的尺寸、最小传动角等则可得唯一解。

具体设计步骤如下：

（1）选取适当的比例尺μ_l，按预定位置画出B₁C₁、B₂C₂、B₃C₃。

（2）连接B₁B₂、B₂B₃、C₁C₂、C₂C₃，并分别作它们的垂直平分线b₁₂、b₂₃、c₁₂、c₂₃，b₁₂和b₂₃的交点即为圆心A，c₁₂和c₂₃的交点即为圆心D。

（3）以点A、D作为两固定铰链的中心，连接AB_1、B₁C₁、C₁D，则AB₁C₁D即为所要设计的四杆机构。

（4）按比例计算出各杆长度。

 

微课

平面四杆机构设计（已知连杆长度与位置）