微课

凸轮机构的工作过程和相关概念

凸轮机构是由凸轮旋转或平移带动从动件进行工作的，因此，设计凸轮结构，首先就要根据实际工作要求确定从动件的运动规律，然后依据从动件运动规律设计出凸轮轮廓曲线。由于工作要求的多样性和复杂性，要求推杆满足的运动规律也是各种各样的。

一、基本术语

如下图所示为一对心直动尖顶推杆盘形凸轮机构。下面根据机构的运动情况定义一些有关的名词和术语。

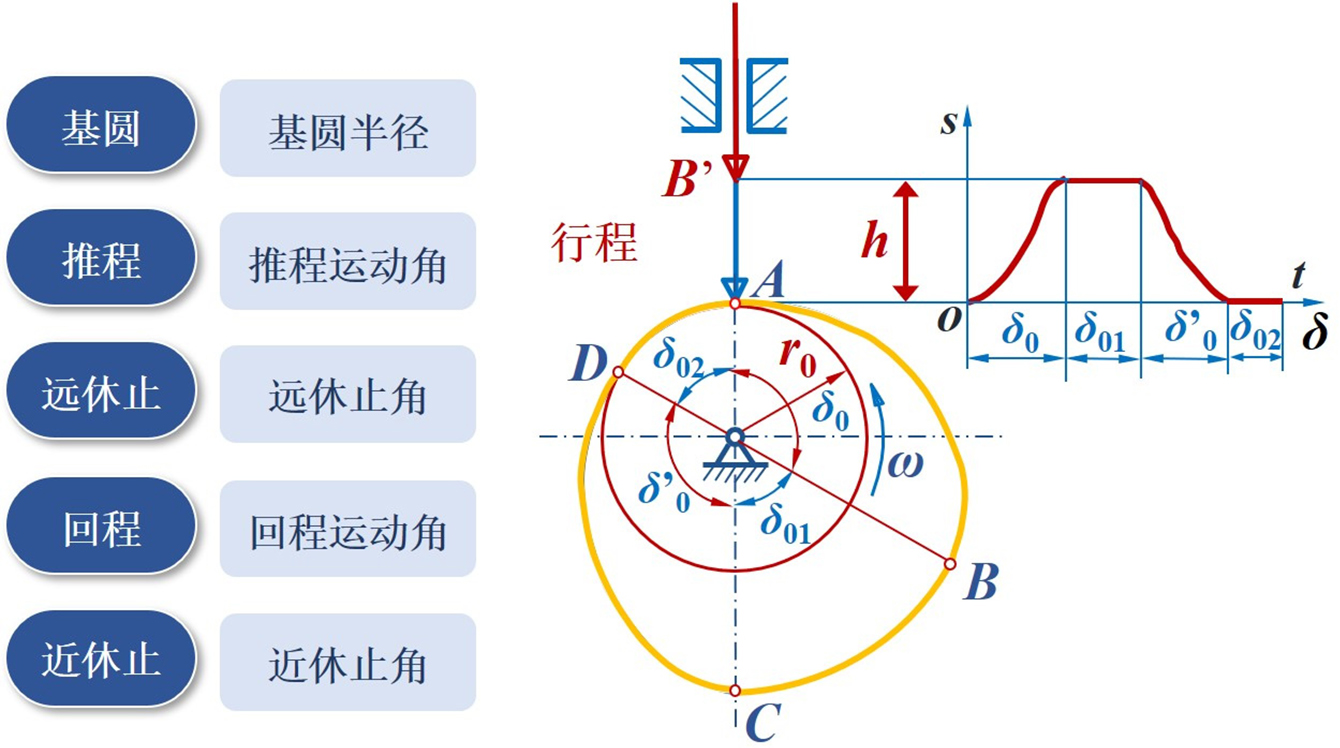
1．基　圆

以凸轮的转动中心O为圆心，以凸轮的最小向径为半径所作的圆称为凸轮的基圆。基圆半径用r_b表示。

2．推　程

当凸轮以等角速度逆时针转动时，从动杆在凸轮廓线的推动下，将由最低位置被推到最高位置，从动杆运动的这一过程称为推程。而相应的凸轮转角称为推程运动角。

3．远休止

凸轮继续转动，从动杆将处于最高位置而静止不动时的这一过程称为远休止。与之相应的凸轮转角称为远休止角。

4．回　程

凸轮继续转动，从动杆从最高位置回到最低位置的这一过程称为回程。相应的凸轮转角称为回程运动角。

5．近休止

当凸轮转过角时，从动杆与凸轮廓线上向径最小的一段圆弧接触，而将处在最低位置静止不动的这一过程称为近休止。称为近休止角。

6．行　程

从动杆在推程或回程中移动的距离h。

7．位移线图

注意

其运动过程的组合是依据工作实际的需要，而不是必须经历四个阶段，可以没有静止阶段，也可以只有一个静止阶段。

二、从动件的运动规律分析

从动件的运动规律取决于凸轮轮廓曲线的形状，不同的从动件运动规律，要求凸轮具有不同形状的轮廓曲线，不同的运动规律对凸轮机构的工作性能也有很大的影响。

因此，在设计凸轮机构时，首先应根据凸轮机构的工作要求和工作条件来选择适当的从动件运动规律。常见的从动件运动规律有：多项式、三角函数、改进型三大类。

（一）多项式运动规律

1．等速（一次多项式）运动规律

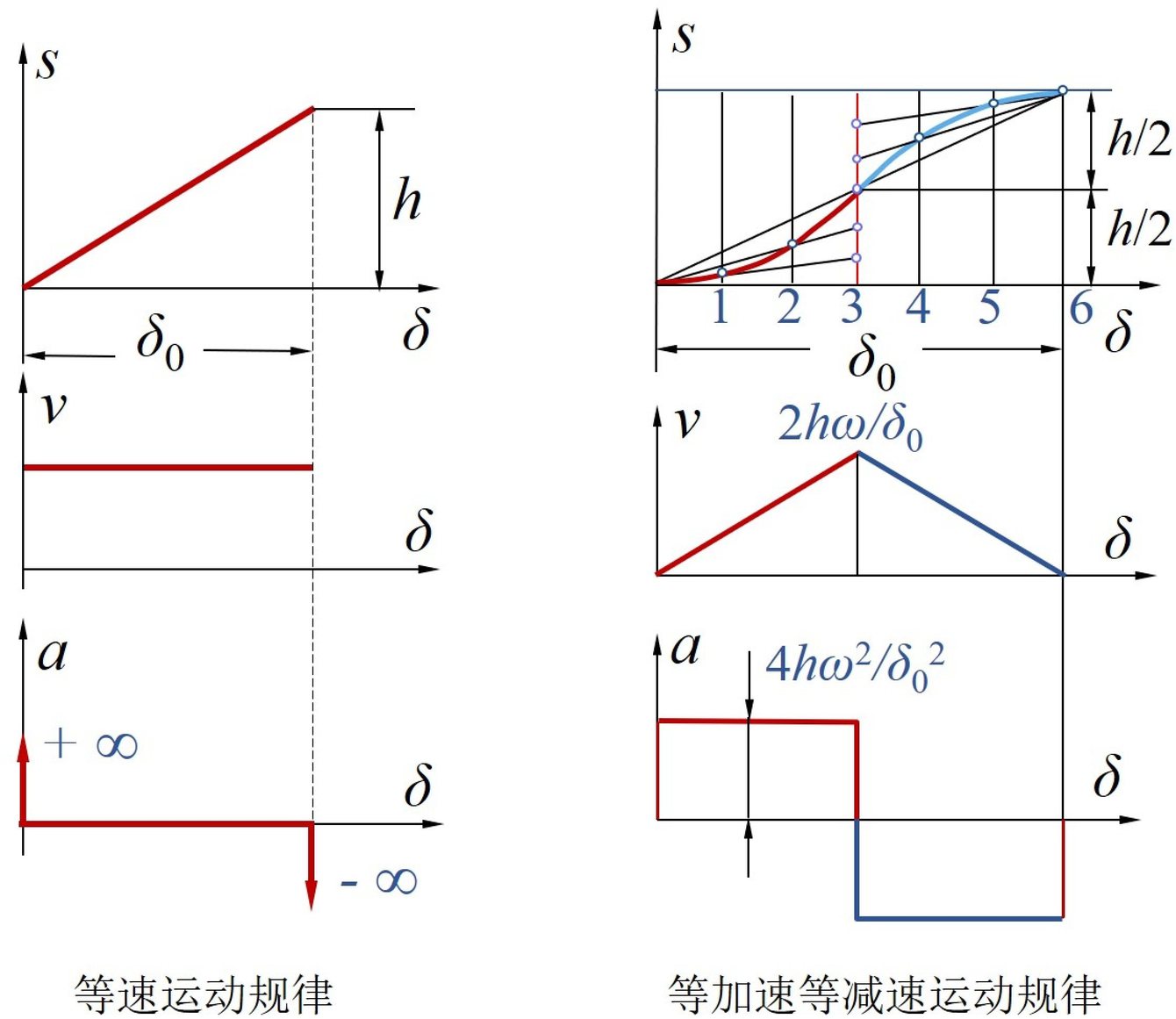
运动开始，ν由0突变为ν₀，加速度a为+∞，运动结束。

冲击特性：始点、末点刚性冲击。

适用场合：低速轻载。

2．等加速—等减速（二次多项式）运动规律

从动件在一个行程中，先作等加速运动，后作等减速运动。

冲击特性：起、中、末点柔性冲击。

适用场合：中低速轻载。

（二）三角函数运动规律

1．余弦加速度（简谐）运动规律

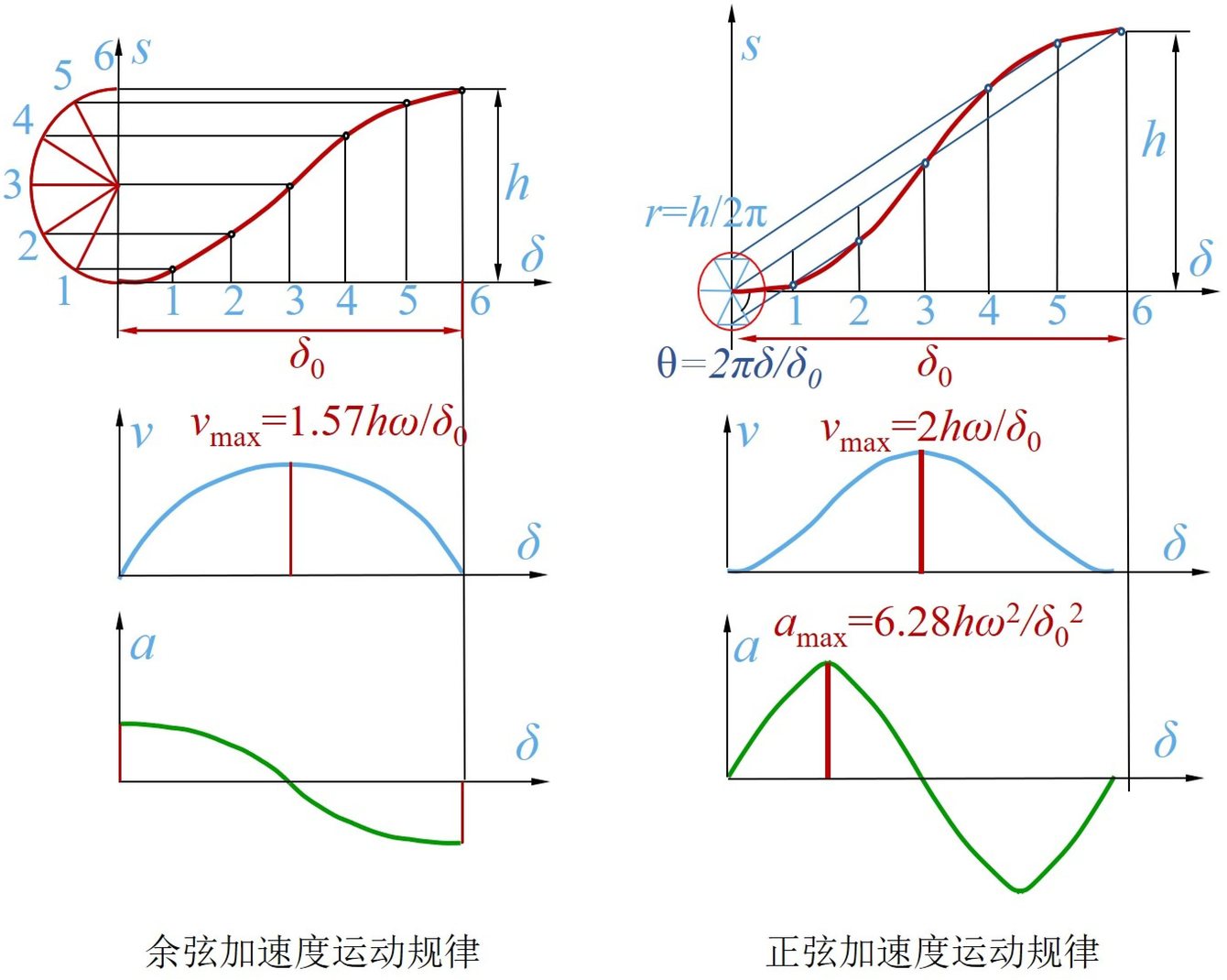
冲击特性：始、末点有柔性冲击。

适用场合：中低速、中轻载。

2．正弦加速度运动规律

速度和加速度曲线都是连续的。

冲击特性：无冲击。

适用场合：高速轻载。

（三）改进型运动规律

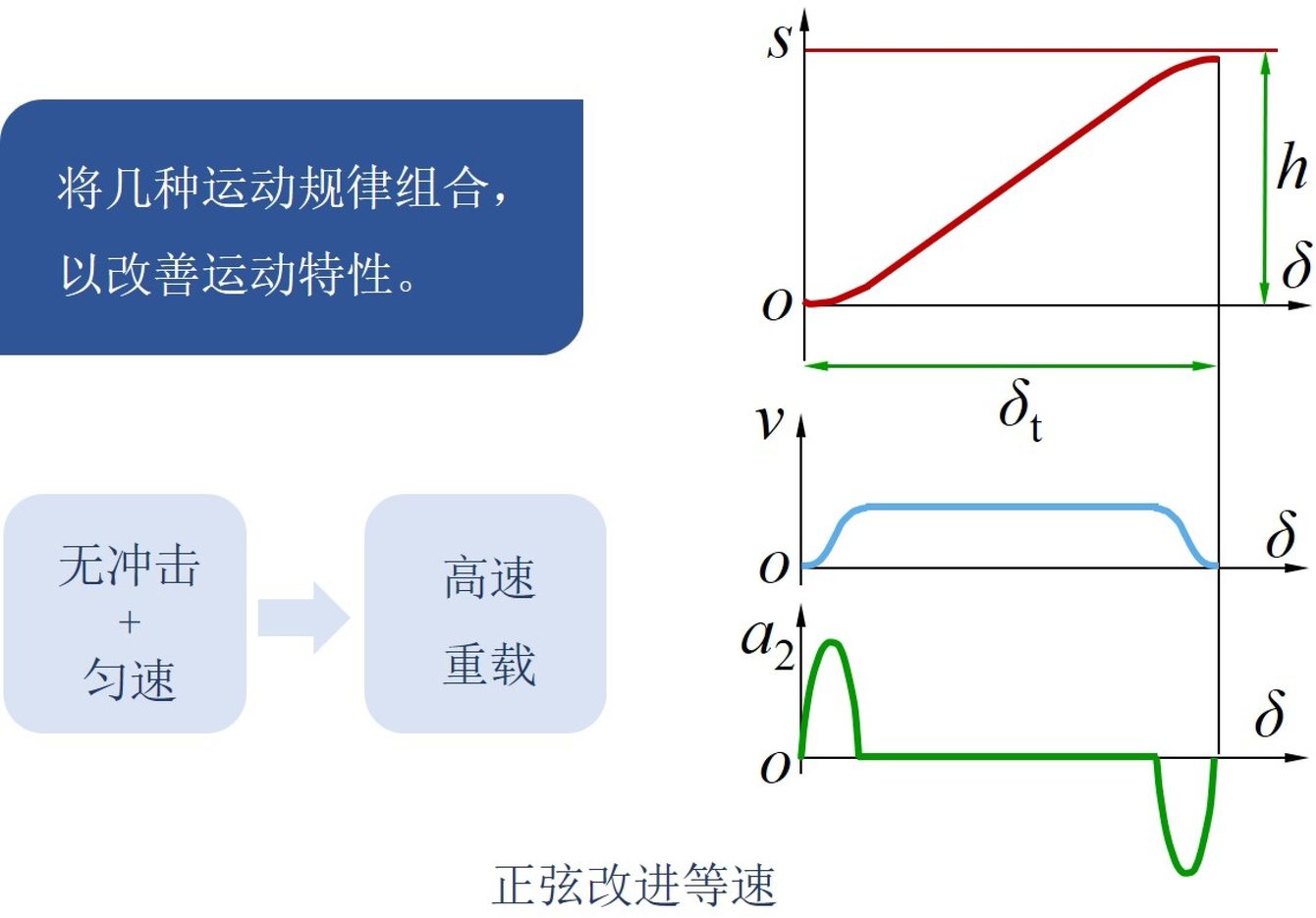
正弦改进等速：将几种运动规律组合，以改善运动特性。

组合的原则：中、低速凸轮机构，s曲线在衔接处相切，以保证v曲线连续；中、高速则还要求v曲线在衔接处相切，以保证a曲线的连续。

（四）从动件运动规律的选择

（1）在选择从动件的运动规律时，应根据机器工作时的运动要求来确定。

（2）对无一定运动要求，只需要从动件有一定位移量的凸轮机构，从便于加工来考虑，可采用圆弧和直线组成的凸轮轮廓。

（3）对于高速机构，应减小惯性力、改善动力性能，可选用正弦加速度运动规律或其他改进型的运动规律。