微课

渐开线的形成及基本性质

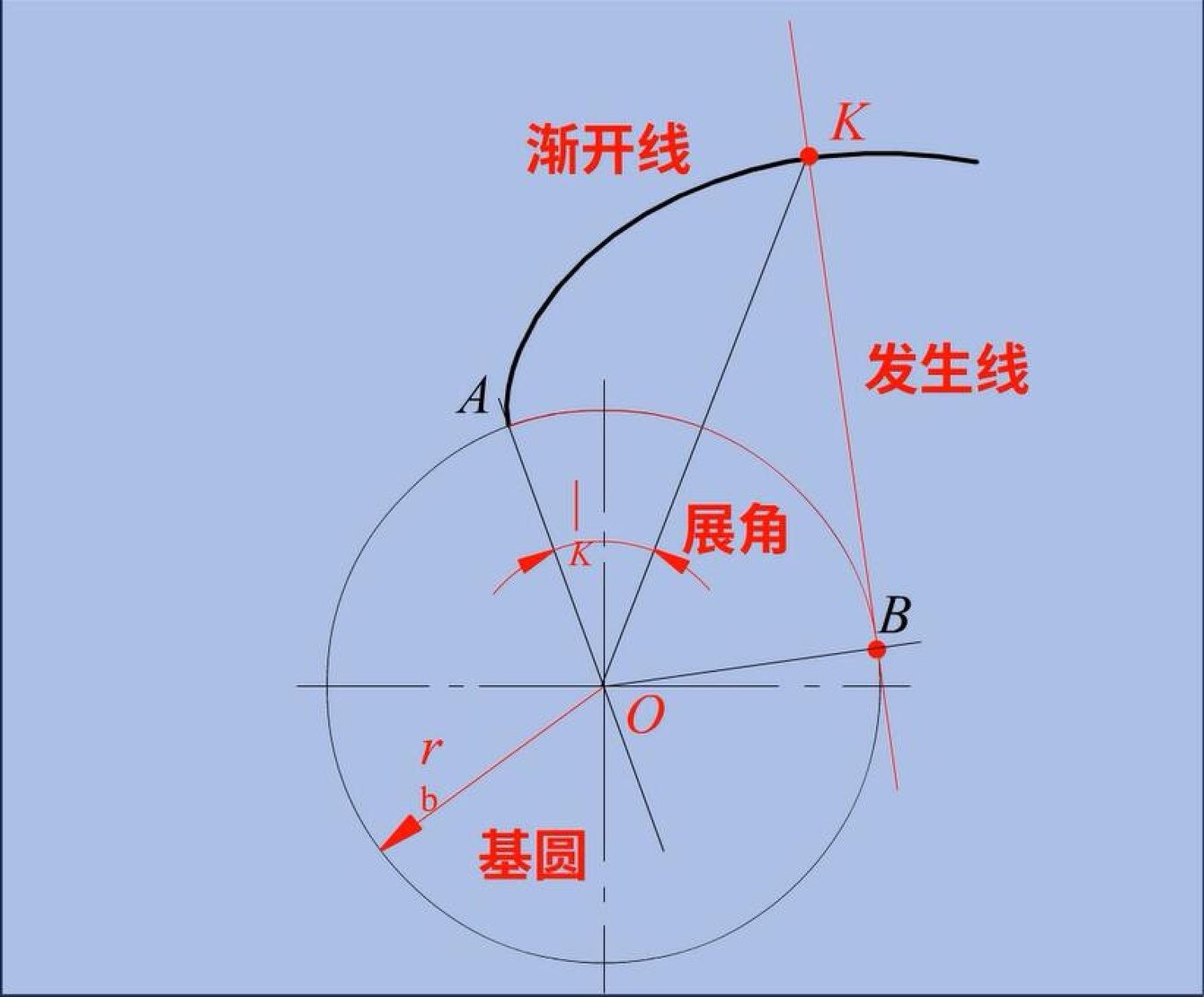
一、渐开线的形成

一条直线BK在圆上作纯滚动作纯滚动时，直线上任意一点K的轨迹称为该圆的渐开线。该圆称为渐开线的基圆，半径用表示，直线BK称为渐开线的发生线。

 

动画

渐开线的形成原理

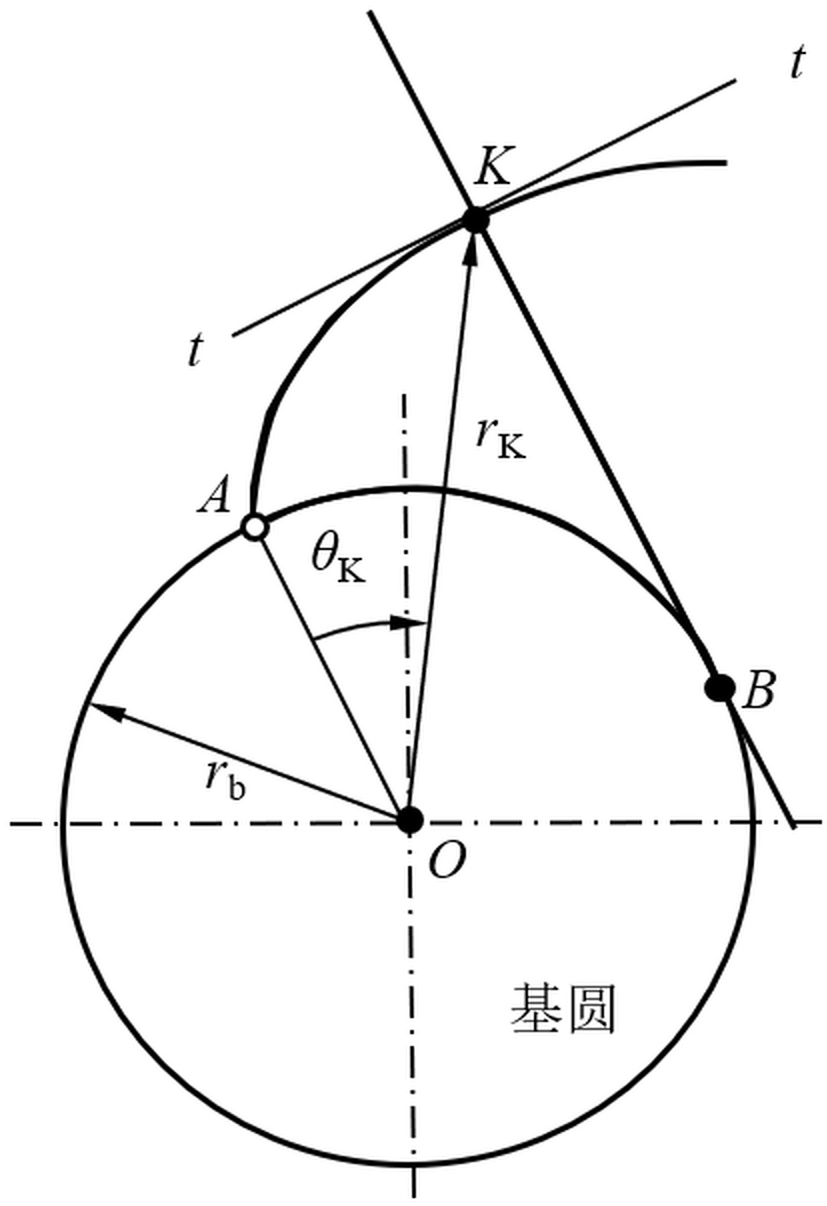
二、渐开线的性质

（1）发生线在基圆上滚过的长度等于基圆上被滚过的弧长，即。

（2）发生线BK是渐开线在K点处的法线。

（3）向径越大，即离基圆圆心越远，渐开线上对应点处的压力角越大。基圆上的压力角等于零。

压力角的概念：渐开线齿廓上任意点的法线与该点的速度方向所夹的锐角称为该点的压力角。

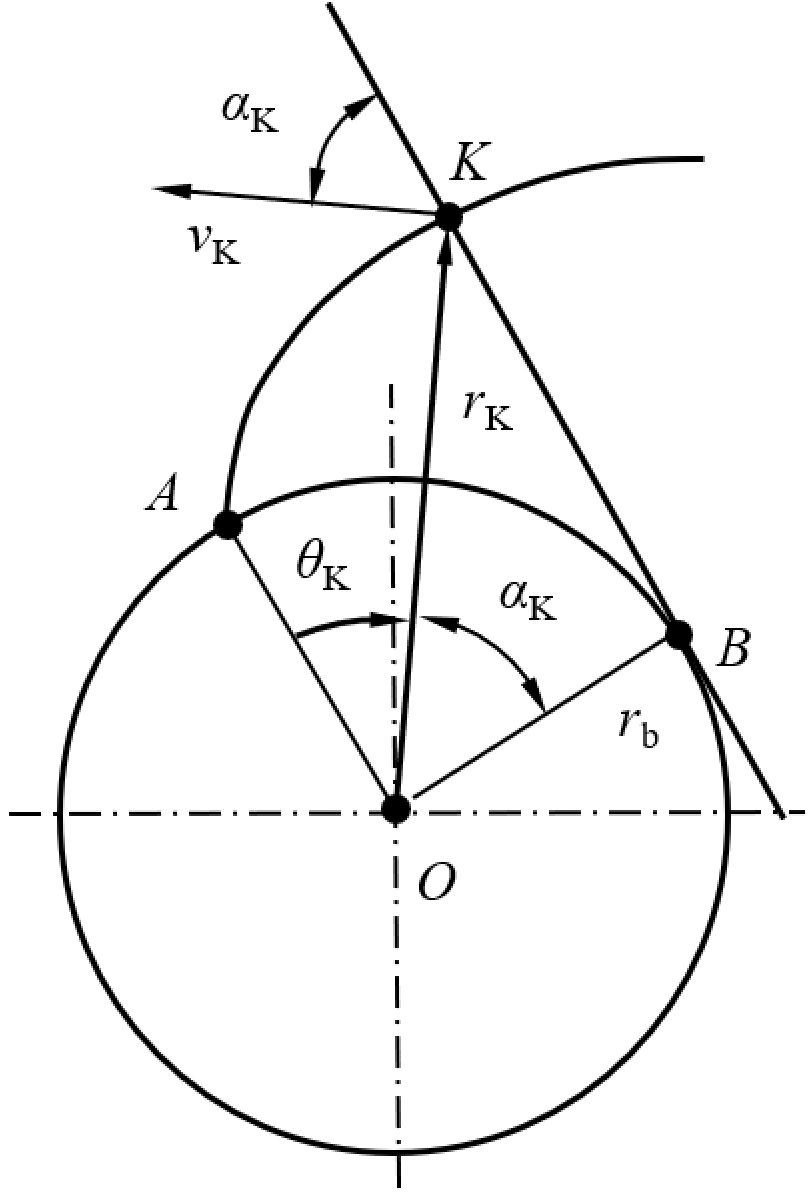
根据渐开线的形成原理，在图示的直角三角形中可以得到如下关系：

当基圆确定时，压力角与向径是正相关关系。

（4）渐开线的形状取决于基圆的大小，基圆越小，渐开线越弯曲，基圆越大，渐开线越平直；当→∞时，渐开线退化为一条直线。

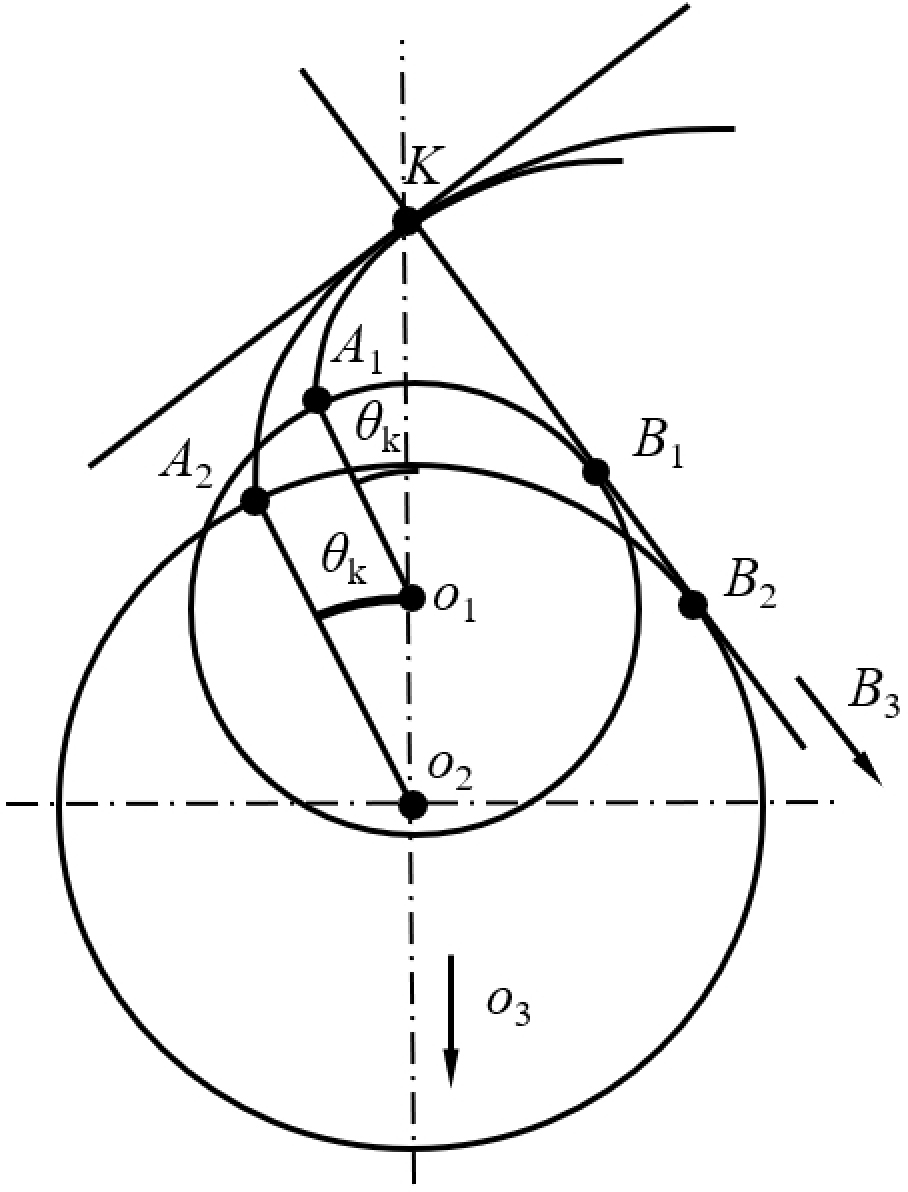
（5）基圆内无渐开线。