一、齿廓啮合基本定律

（一）齿廓啮合基本定律证明

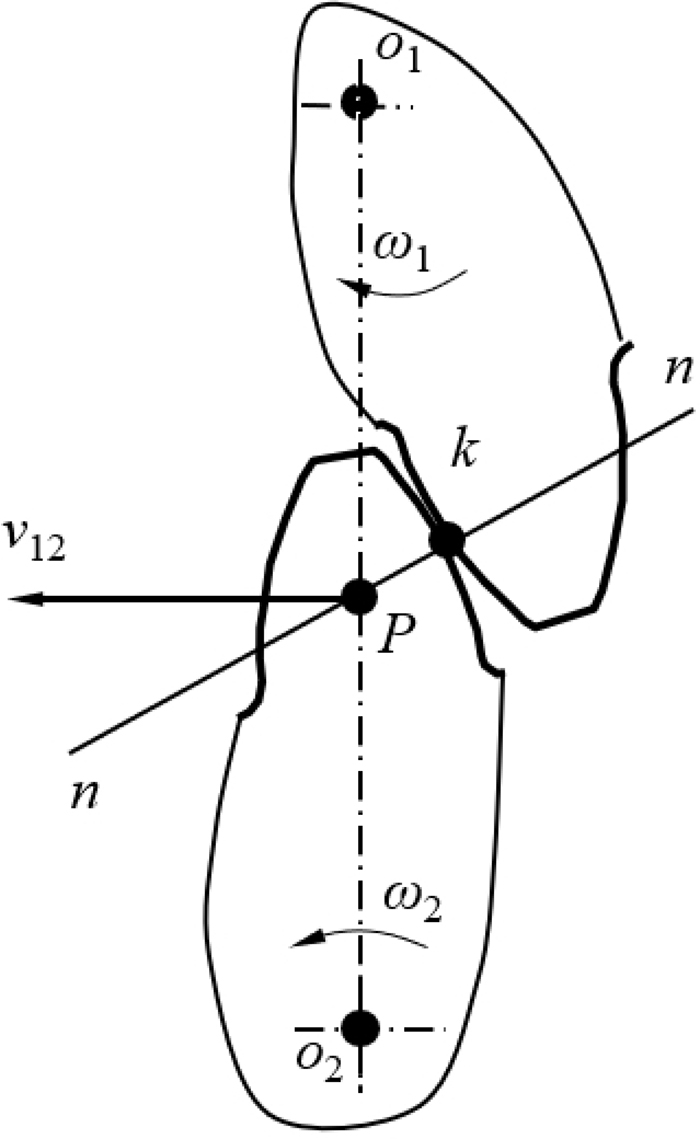
一对齿廓在点K接触时，作法线n-n，根据三心定理可知：法线n-n与连心线的交点P为相对速度瞬心。

P点的速度为

两齿轮的传动比：

从上式可知，相互啮合传动的一对齿轮，在任一瞬时的传动比等于该瞬时两齿轮连心线被其啮合齿廓接触线的公法线所分割的两线段长度的反比。这一定律称为齿廓啮合基本定律。

（二）共轭齿廓的概念

所谓共轭齿廓：相互连续接触传动并能实现预定传动比规律的一对齿廓。

理论上有无穷多对共轭齿廓，在生产中，除了考虑传动比外，还要考虑设计、制造、安装精度和使用要求等。最常用的是渐开线，其次是摆线、变态摆线或圆弧齿廓等。

对齿轮传动的基本要求是保证瞬时传动比恒定，即：

这样可以（1）避免变速引起的惯性力矩；（2）避免振动。

二、渐开线齿廓的啮合特点

（一）瞬时传动比恒定

两齿廓在任意点K啮合时，过K作两齿廓的法线，是基圆的切线，为定直线。

两轮中心连线也为定直线，故交点P必为定点。

根据齿廓啮合基本定律：

瞬时传动比恒定的工程意义：传动比为常数可减少因速度变化所产生的附加动载荷、振动和噪音，延长齿轮的使用寿命，提高机器的工作精度。

（二）齿廓间正压力方向不变

是啮合点的轨迹，称为啮合线。啮合线与节圆公切线之间的夹角α’称为啮合角。实际上，啮合角α’就是渐开线在节圆上的压力角。

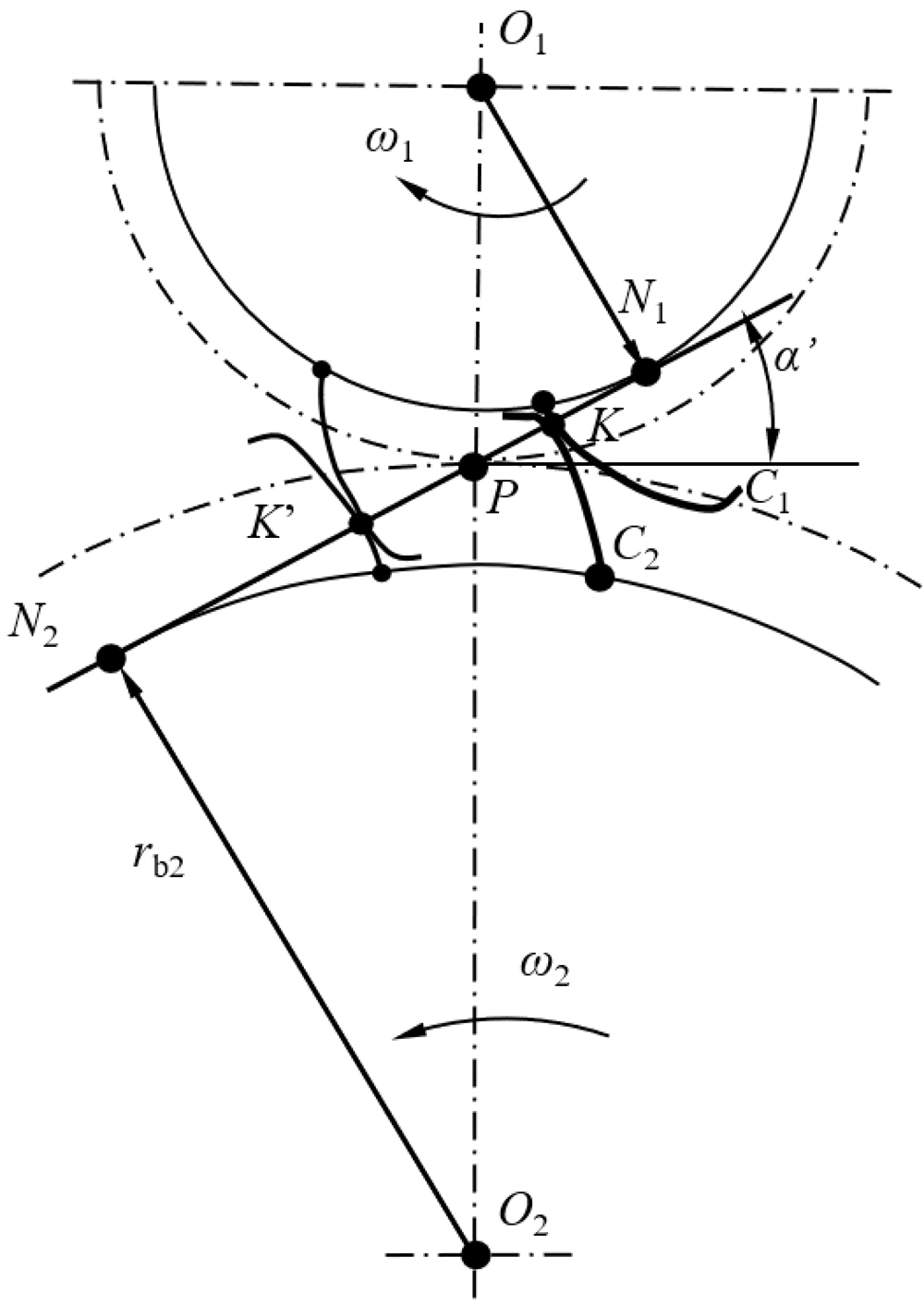
由渐开线的性质可知：啮合线又是接触点的法线，正压力总是沿法线方向，故正压力方向不变。该特性对传动的平稳性有利。

（三）渐开线齿廓传动中心距可分性

在图示中，两个直角三角形相似，

上式表明，渐开线齿轮的传动比等于两轮基圆半径的反比，其基圆的大小是不变的，所以当两轮的实际中心距与设计中心距不一致时，两轮的传动比却保持不变。这一特性称为传动的可分性，对加工和装配很有利。

正是由于上述优点，渐开线齿轮传动获得十分广泛应用。

三、正确啮合条件

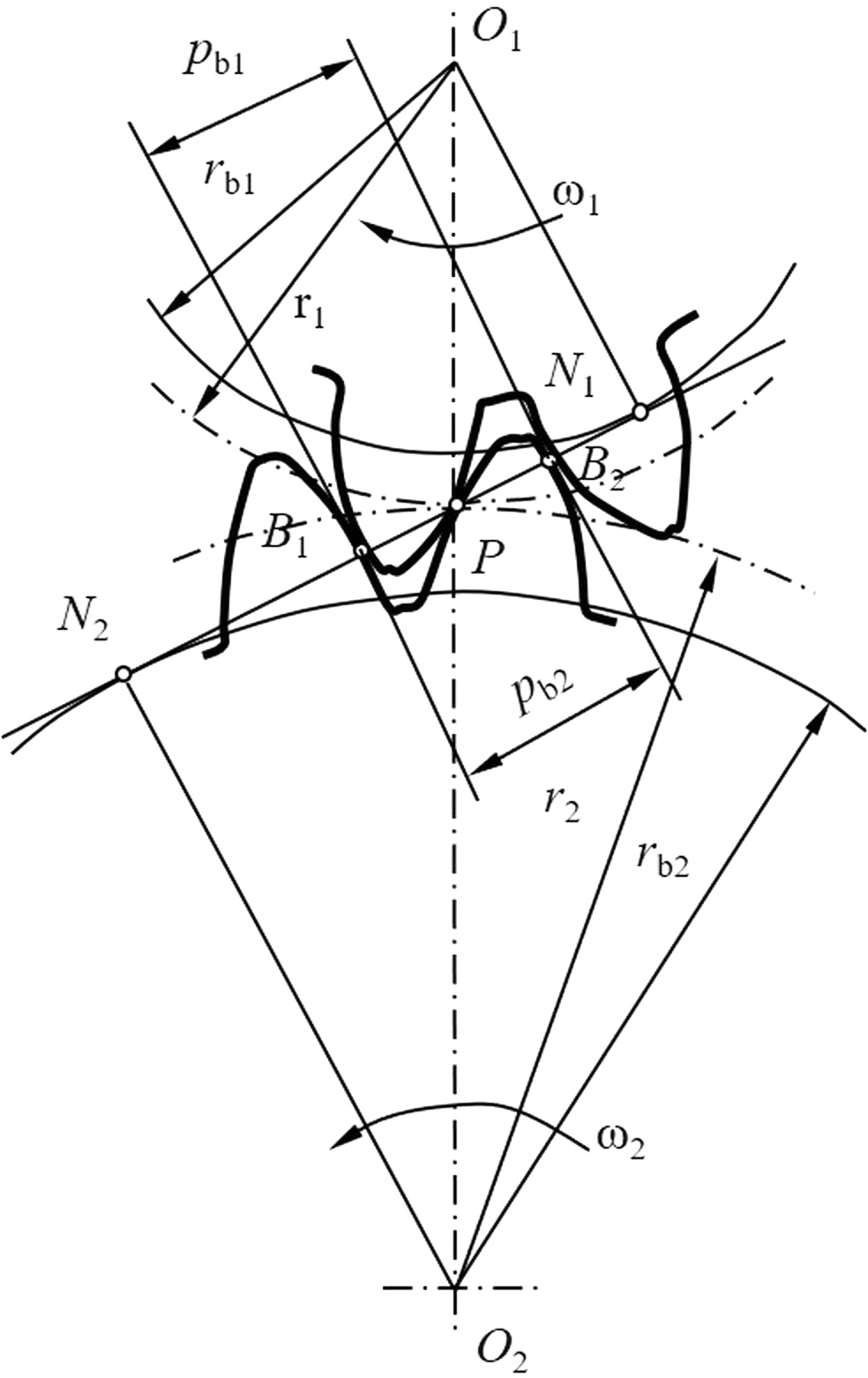
两齿轮的相邻两对轮齿分别B₁在和B₂时接触，才能使两个渐开线齿轮搭配起来并正确的传动。

为了保证前后两对齿轮能在啮合线上同时接触而又不产生干涉，则必须使两轮的相邻两齿同侧齿廓沿啮合线上距离（法向齿距）相等。由渐开线性质可知，法向齿距与基圆齿距相等，即 P_b1=P_b2。

又由，由此可得两齿轮正确啮合的条件为：

因m和α都取标准值。

所以：

结论：一对渐开线齿轮的正确啮合条件是模数和压力角应分别相等。

也正因为模数和压力角应分别相等，一对齿轮的传动比才可以推导出等于齿数反比：

四、两齿轮的啮合过程和连续传动的条件

（一）一对渐开线轮齿的啮合过程

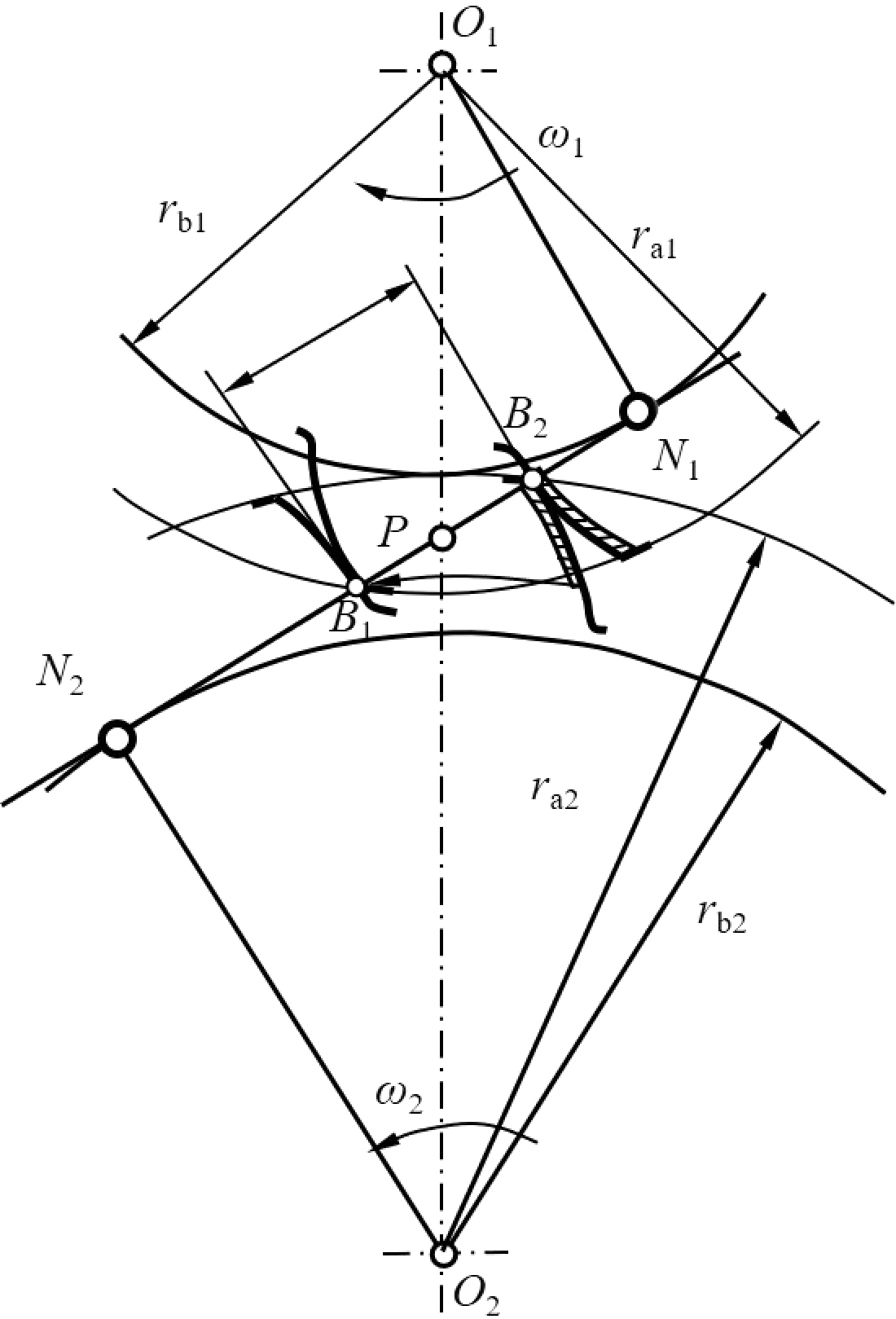
一对轮齿在啮合线上啮合的起始点——从动轮2的齿顶圆与啮合线N₁N₂的交点B₂。

一对轮齿在啮合线上啮合的终止点——主动轮1的齿顶圆与啮合线N₁N₂的交点B₁。

（二）连续传动条件及重合度

为保证连续定角速比传动的条件为：

定义：为重合度。

一对齿轮的连续传动条件是：。

从理论上讲，重合度为1就能保证连续传动，但齿轮制造和安装有误差，所以实际工程上，则要求ε_α≥[ε_α]。

式中[ε_α]为许用重合度，常用推荐值：

一般制造业[ε_α]=1.4。

汽车、拖拉机[ε_α]=1.1～1.2。

金属切削机床[ε_α]=1.3。